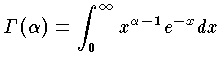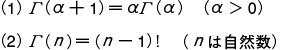|
|
| 1行目: |
1行目: |
| − | '''オイラー積'''(-せき、{{lang-en-short|Euler product}})は[[ディリクレ級数]]を[[素数]]に関する[[総乗]]の形で表した[[無限積]]である。ディリクレ級数の一種の[[ベルンハルト・リーマン|リーマン]]の[[リーマンゼータ関数|ゼータ関数]]についてこの無限積が成り立つことを証明した[[レオンハルト・オイラー]]の名前にちなむ。ディリクレ級数は以下の式の左辺で定義され、右辺がオイラー積表示である。 | + | '''オイラー積'''(-せき、{{lang-en-short|Euler product}}) |
| − | :<math>\sum_{n=1}^\infty \frac{a(n)}{n^s} = \prod_{p} \frac{1}{1- a(p)/p^s}</math>
| |
| | | | |
| − | ''a''(''n'') は ''n'' に関する乗法的関数、''p'' は全ての素数にわたり、変数 ''s'' は[[複素数]]である。このような表示が成り立つためには ''a''(''n'') が ''a''(1) = 1, ''a''(''mn'') = ''a''(''m'') ''a''(''n'') を全ての[[自然数]] ''m'', ''n'' について満たさなければならない。一般に ''s'' の[[実部]] Re(''s'') に対して <math>\operatorname{Re}(s) > C</math> ならば上記の級数(または無限積)が[[絶対収束]]するようなある実数の定数 ''C'' が存在することが知られている。
| + | 第2種オイラー積分ともいう。 α>0 で定義された関数 |
| | | | |
| − | ''a''(''n'') = 1 とおいたとき
| + | [[ファイル:Gamma function.gif]] |
| − | :<math>\sum_{n=1}^\infty \frac{1}{n^s} = \prod_{p} \frac{1}{1- 1/p^s}</math>
| |
| − | となる。これがリーマンゼータ関数のオイラー積表示である。すなわち
| |
| − | :<math>\frac {1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots = \left( \frac{1}{1- \frac{1}{2^s}} \right) \left( \frac{1}{1- \frac{1}{3^s}} \right) \left( \frac{1}{1- \frac{1}{5^s}} \right) \cdots</math>
| |
| − | これは s の実部が 1 より大きいとき[[収束]]する。
| |
| | | | |
| − | == ゼータ関数に対するオイラー積 ==
| + | をガンマ関数という。ガンマ関数は,次の性質をもつ。 |
| − | リーマンゼータ関数のオイラー積は[[1737年]]にオイラーによって発見された。まずゼータ関数 ''ζ''(''s'') は ''s'' の実部が1より大きいとき、次のように定義される。
| |
| − | :<math> \zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s} = \frac {1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots </math>
| |
| | | | |
| − | ここで両辺に最小の素数2の-''s''乗 1/2''<sup>s</sup>'' をかけると
| + | [[ファイル:Gamma function2.gif]] |
| − | :<math>\frac {1}{2^s} \zeta (s) = \frac {1}{2^s} + \frac{1}{4^s} + \frac{1}{6^s} + \cdots</math> | |
| − | となり、辺々引くと
| |
| − | :<math> \left(1- \frac {1}{2^s}\right) \zeta (s) = \frac {1}{1^s} + \frac{1}{3^s} + \frac{1}{5^s} + \cdots</math>
| |
| | | | |
| − | この両辺に今度は2の次の素数3の-''s''乗 1/3<sup>''s''</sup> をかけると
| + | この (2) の性質からガンマ関数は,階乗を拡張した関数ということができる。この関数は,オイラーによって発見されたもので,ベータ関数と並んでオイラー積分の名が与えられている。 |
| | | | |
| − | :<math> \frac {1}{3^s} \left(1- \frac {1}{2^s}\right) \zeta (s) = \frac {1}{3^s} + \frac{1}{9^s} + \frac{1}{15^s} + \cdots</math>
| + | {{テンプレート:20180815sk}} |
| − | となり、再び辺々引くと
| |
| − | :<math> \left(1- \frac {1}{2^s}\right) \left(1- \frac {1}{3^s}\right) \zeta (s) = \frac {1}{1^s} + \frac{1}{5^s} + \frac{1}{7^s} + \cdots</math>
| |
| − | | |
| − | 以下同様に次々と素数の-''s''乗を両辺にかけて前の式から引くという操作を続けると右辺の 1/1''<sup>s</sup>'' 以外の項は([[素因数分解の一意性]]によって)消えるので
| |
| − | | |
| − | :<math> \left(1- \frac {1}{2^s}\right) \left(1- \frac {1}{3^s}\right) \left(1- \frac {1}{5^s}\right) \left(1- \frac {1}{7^s}\right) \cdots \zeta (s) = \frac {1}{1^s} = 1</math>
| |
| − | したがってゼータ関数は以下の形で表現される。
| |
| − | :<math>\zeta (s) = \frac{1} {{(1- \frac{1}{2^s})} {(1- \frac{1}{3^s})} {(1- \frac{1}{5^s})} {(1- \frac{1}{7^s})} \cdots }</math>
| |
| − | | |
| − | 上記の式に形式的に ''s''=1 を代入すると
| |
| − | :<math>\zeta (1) = \frac{1} {{(1- \frac{1}{2})} {(1- \frac{1}{3})} {(1- \frac{1}{5})} {(1- \frac{1}{7})} \cdots }</math> | |
| − | ここで左辺は[[調和級数]]であり、正の無限大に[[発散]]するので右辺も同様に発散すると考えられる。このことから素数の個数は有限ではないことが導かれる。なぜならもし素数が有限個なら右辺はある定数になるからである。
| |
| − | | |
| − | == さまざまな関数に対するオイラー積 ==
| |
| − | ゼータ関数については上記のように
| |
| − | :<math> \sum_{n=1}^\infty \frac {1}{n^s} = \frac{1} {{(1- \frac{1}{2^s})} {(1- \frac{1}{3^s})} {(1- \frac{1}{5^s})} {(1- \frac{1}{7^s})} \cdots } = \zeta (s) </math>
| |
| − | である。いっぽう[[w:Liouville function|リウヴィル関数]] λ(n) については
| |
| − | :<math> \sum_{n=1}^\infty \frac {\lambda (n)}{n^s} = \frac{1} {{(1+ \frac{1}{2^s})} {(1+ \frac{1}{3^s})} {(1+ \frac{1}{5^s})} {(1+ \frac{1}{7^s})} \cdots } = \frac {\zeta (2s)} {\zeta (s)} </math>
| |
| − | [[メビウス関数]] μ(n) では
| |
| − | :<math> \sum_{n=1}^\infty \frac {\mu (n)}{n^s} = \left( 1- \frac{1}{2^s} \right) \left( 1- \frac{1}{3^s} \right) \left( 1- \frac{1}{5^s} \right) \left( 1- \frac{1}{7^s} \right) \cdots = \frac {1}{\zeta (s)}</math>
| |
| − | や左辺の分子の[[絶対値]]をとった
| |
| − | :<math> \sum_{n=1}^\infty \frac {|\mu (n)|}{n^s} = \left( 1+ \frac{1}{2^s} \right) \left( 1+ \frac{1}{3^s} \right) \left( 1+ \frac{1}{5^s} \right) \left( 1+ \frac{1}{7^s} \right) \cdots = \frac {\zeta (s)} {\zeta (2s)} </math>
| |
| − | という無限積が知られている。
| |
| − | | |
| − | == 関連項目 ==
| |
| − | * [[ディリクレ級数]]
| |
| − | * [[リーマンゼータ函数|ゼータ関数]]
| |
| − | * [[レオンハルト・オイラー]]
| |
| − | | |
| − | == 外部リンク ==
| |
| − | * [http://mathworld.wolfram.com/EulerProduct.html Euler Product] -[[MathWorld]]
| |
| − | * [http://planetmath.org/?op=getobj&from=objects&id=5609 Euler product] -[[PlanetMath]]
| |
| − | | |
| − | {{math-stub}}
| |
| | {{DEFAULTSORT:おいらあせき}} | | {{DEFAULTSORT:おいらあせき}} |
| | [[Category:数論|おいらあせき]] | | [[Category:数論|おいらあせき]] |
| | [[Category:数学に関する記事|おいらあせき]] | | [[Category:数学に関する記事|おいらあせき]] |
| | [[Category:レオンハルト・オイラー]] | | [[Category:レオンハルト・オイラー]] |