|
|
| 1行目: |
1行目: |
| − | [[Image:Apollonius circle definition labels.svg|thumb|アポロニウスの円。AP:BPが一定になるようにPを動かすと軌跡は円を描く。]] | + | [[ファイル:アポロニウスの円.gif|サムネイル]] |
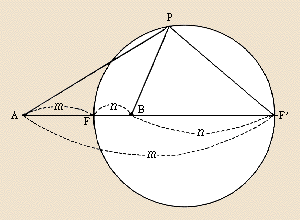
| − | '''アポロニウスの円'''(アポロニウスのえん)は、2[[定点]]A・Bをとり、点PをAP:BPが一定となるように(但しAP≠BP)したときの点Pの[[軌跡 (数学)|軌跡]]である。[[ペルガのアポロニウス]]の名前を残す。 | + | '''アポロニウスの円'''(アポロニウスのえん) |
| | | | |
| − | == 証明 ==
| + | アポロニオスの軌跡ともいう。平面上の2定点をA ,B ,線分 AB を内分および外分する一定の比を <i>m</i>:<i>n</i> ( <i>m</i>≠<i>n</i> ) ,その内分点および外分点をそれぞれ F ,F' とすれば,A ,B からの距離の比が <i>m</i>:<i>n</i> であるような点P の軌跡は,線分 FF' を直径とする円である。この円をアポロニオスの円という。 |
| − | === 初等幾何による証明 ===
| |
| − | [[画像:アポロニウスの円.svg|350px]]
| |
| − | | |
| − | 点PをAP:BPが一定となるようにしたときの点Pの[[軌跡 (数学)|軌跡]]のうち、線分ABの上の点をQ、ABの延長線上の点をRとすると、
| |
| − | :AQ:QB=AP:PB
| |
| − | :AR:RB=AP:PB
| |
| − | 内角と外角の二等分線の関係の逆より、PQとPRはそれぞれ∠APBの内角と外角の二等分線である。
| |
| − | よって、∠QPR=90°
| |
| − | ゆえに、点Pの軌跡は線分QRを直径とする円である。
| |
| − | | |
| − | === ベクトルによる証明(1) ===
| |
| − | ''m'', ''n'' を互いに異なる正の実数とする。線分ABを ''m'' : ''n'' に内分する点を Q、外分する点をRとすると、
| |
| − | :<math>\overrightarrow{\mathrm{PQ}} = \frac{n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}}}{n+m},\ \overrightarrow{\mathrm{PR}} = \frac{n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}}}{n-m}.</math>
| |
| − | このとき、
| |
| − | :<math>\mathrm{PA} : \mathrm{PB} = m : n.</math>
| |
| − | :<math>\Leftrightarrow n|\overrightarrow{\mathrm{PA}}| = m|\overrightarrow{\mathrm{PB}}|.</math>
| |
| − | :<math>\Leftrightarrow n^2|\overrightarrow{\mathrm{PA}}|^2 = m^2|\overrightarrow{\mathrm{PB}}|^2.</math>
| |
| − | :<math>\Leftrightarrow (n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}})\cdot (n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}})=0.</math>
| |
| − | :<math>\Leftrightarrow \frac{n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}}}{n+m}\cdot \frac{n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}}}{n-m}=0.</math>
| |
| − | :<math>\Leftrightarrow \overrightarrow{\mathrm{PQ}} \cdot \overrightarrow{\mathrm{PR}} =0.</math>
| |
| − | :<math>\Leftrightarrow \overrightarrow{\mathrm{PQ}} = \vec{0} \vee \overrightarrow{\mathrm{PR}} =\vec{0} \vee \overrightarrow{\mathrm{PQ}} \perp \overrightarrow{\mathrm{PR}}.</math>
| |
| − | :<math>\Leftrightarrow \mathrm{P}=\mathrm{Q} \vee \mathrm{P}=\mathrm{R} \vee \angle{\mathrm{QPR}}=90^\circ.</math>
| |
| − | したがって、点Pの軌跡は線分QRを直径とする円になる。
| |
| − | | |
| − | === ベクトルによる証明(2) ===
| |
| − | 線分QRの中点をOとすると、
| |
| − | :<math>\overrightarrow{\mathrm{OQ}} = -\frac{1}{2}\overrightarrow{\mathrm{QR}}, \ \overrightarrow{\mathrm{OR}} = \frac{1}{2}\overrightarrow{\mathrm{QR}}.</math>
| |
| − | したがって、
| |
| − | :<math>\overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{\mathrm{PR}} = 0.</math>
| |
| − | :<math>\Leftrightarrow (\overrightarrow{\mathrm{PO}}+\overrightarrow{\mathrm{OQ}})\cdot (\overrightarrow{\mathrm{PO}}+\overrightarrow{\mathrm{OR}}) = 0.</math>
| |
| − | :<math>\Leftrightarrow (\overrightarrow{\mathrm{PO}}-\frac{1}{2}\overrightarrow{\mathrm{QR}})\cdot (\overrightarrow{\mathrm{PO}}+\frac{1}{2}\overrightarrow{\mathrm{QR}}) = 0.</math>
| |
| − | :<math>\Leftrightarrow |\overrightarrow{\mathrm{PO}}|^2 = \left( \frac{1}{2}\right)^2|\overrightarrow{\mathrm{QR}}|^2.</math>
| |
| − | :<math>\Leftrightarrow \mathrm{PO} = \frac{1}{2}\mathrm{QR}.</math>
| |
| − | これより、点Pの軌跡は線分QRの中点Oを中心とする半径 <math>\frac{1}{2}\mathrm{QR}</math> の円、すなわち線分QRを直径とする円になる。
| |
| − | | |
| − | === アポロニウスの円の中心 ===
| |
| − | 線分QRの中点をOとすると、点Oはアポロニウスの円の中心となり、
| |
| − | :<math>\begin{align}\overrightarrow{\mathrm{PO}} &= \frac{\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{PR}}}{2} \\ &= \frac{1}{2}\left( \frac{n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}}}{n+m}+\frac{n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}}}{n-m} \right) \\ &= \frac{(n-m)(n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}})+(n+m)(n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}})}{2(n+m)(n-m)} \\ &= \frac{2n^2\overrightarrow{\mathrm{PA}}-2m^2\overrightarrow{\mathrm{PB}}}{2(n^2-m^2)} \\ &= \frac{n^2\overrightarrow{\mathrm{PA}}-m^2\overrightarrow{\mathrm{PB}}}{n^2-m^2}.\end{align}</math>
| |
| − | すなわち、点Oは線分ABを <math>m^2 : n^2</math> に外分する点になる。
| |
| − | | |
| − | === アポロニウスの円の半径 ===
| |
| − | アポロニウスの円の半径を ''r'' とする。ここで平方完成
| |
| − | | |
| − | :<math>\begin{align}\frac{1}{2}\overrightarrow{\mathrm{QR}} &= \frac{\overrightarrow{\mathrm{PR}}-\overrightarrow{\mathrm{PQ}}}{2} \\ &= \frac{1}{2}\left( \frac{n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}}}{n-m}-\frac{n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}}}{n+m} \right) \\ &= \frac{(n+m)(n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}})-(n-m)(n\overrightarrow{\mathrm{PA}}+m\overrightarrow{\mathrm{PB}})}{2(n+m)(n-m)} \\ &= \frac{2mn\overrightarrow{\mathrm{PA}}-2mn\overrightarrow{\mathrm{PB}}}{2(n^2-m^2)} \\ &= \frac{mn(\overrightarrow{\mathrm{PB}}-\overrightarrow{\mathrm{PA}})}{m^2-n^2} \\ &= \frac{mn}{m^2-n^2}\overrightarrow{\mathrm{AB}}.\end{align}</math>
| |
| − | | |
| − | 定義より、
| |
| − | | |
| − | :<math>\begin{align}\overrightarrow{\mathrm{AR}} &= \overrightarrow{\mathrm{PR}}-\overrightarrow{\mathrm{PA}} \\ &= \frac{n\overrightarrow{\mathrm{PA}}-m\overrightarrow{\mathrm{PB}}}{n-m}-\overrightarrow{\mathrm{PA}} \\ &= \frac{m}{n-m}(\overrightarrow{\mathrm{PA}}-\overrightarrow{\mathrm{PB}}) \\ &= \frac{m}{m-n}\overrightarrow{\mathrm{AB}}, \\ \overrightarrow{\mathrm{QB}} &= \frac{n}{m+n}\overrightarrow{\mathrm{AB}}, \\ \overrightarrow{\mathrm{AO}} &= \overrightarrow{\mathrm{PO}}-\overrightarrow{\mathrm{PA}} \\ &= \frac{n^2\overrightarrow{\mathrm{PA}}-m^2\overrightarrow{\mathrm{PB}}}{n^2-m^2}-\overrightarrow{\mathrm{PA}} \\ &= \frac{m^2}{n^2-m^2}(\overrightarrow{\mathrm{PA}}-\overrightarrow{\mathrm{PB}}) \\ &= \frac{m^2}{m^2-n^2}\overrightarrow{\mathrm{AB}}, \\ \overrightarrow{\mathrm{BO}} &=
| |
| − | \overrightarrow{\mathrm{PO}}-\overrightarrow{\mathrm{PB}} \\ &= \frac{n^2\overrightarrow{\mathrm{PA}}-m^2\overrightarrow{\mathrm{PB}}}{n^2-m^2}-\overrightarrow{\mathrm{PB}} \\ &= \frac{n^2}{n^2-m^2}(\overrightarrow{\mathrm{PA}}-\overrightarrow{\mathrm{PB}}) \\ &= \frac{n^2}{m^2-n^2}\overrightarrow{\mathrm{AB}}.\end{align}</math>
| |
| − | | |
| − | したがって、
| |
| − | :<math>r = \left|\frac{mn}{m^2-n^2}\right|\cdot\mathrm{AB} = \frac{\mathrm{AR}\cdot \mathrm{QB}}{\mathrm{AB}} = \sqrt{\mathrm{OA}\cdot \mathrm{OB}}.</math>
| |
| − | | |
| − | ==アポロニウスの問題に対する解==
| |
| − | [[アポロニウスの問題]]に対する解はアポロニウスの円とも呼ばれる。
| |
| − | | |
| − | == 外部リンク ==
| |
| − | {{Commonscat|Circles of Apollonius}}
| |
| − | *[https://www.chart.co.jp/subject/sugaku/suken_tsushin/33/33-8.pdf アポロニウスの円の中心について] - 『[[数研通信]]』33号
| |
| − | *[http://izumi-math.jp/F_Nakamura/aporo_3/aporo_3.htm アポロニウスの円の中心と半径]
| |
| − | *[http://izumi-math.jp/H_Yamazaki/aporo/aporo.htm アポロニウスの円~定義を少し広げる試み~]
| |
| − | *[http://sshmathgeom.private.coocan.jp/highschool/problem12.html 高校数学で注意して欲しいこと 2. 軌跡]
| |
| − | *[http://izumi-math.jp/F_Nakamura/toubun/toubun.pdf 角の二等分線の性質を狩る]
| |
| − | *{{高校数学の美しい物語|title=アポロニウスの円の証明と応用|urlname=apollonius}}
| |
| − | *[http://math-info.criced.tsukuba.ac.jp/Forall/project/2000/Apollonius-fl/Apollonius-index.htm アポロニウスの接円問題の探究] - [[筑波大学]]数学教育研究室 代数・幾何・微積 For All プロジェクト
| |
| | | | |
| | {{DEFAULTSORT:あほろにうすのえん}} | | {{DEFAULTSORT:あほろにうすのえん}} |
| | + | {{テンプレート:20180815sk}} |
| | [[Category:円 (数学)]] | | [[Category:円 (数学)]] |
| | [[Category:初等幾何学]] | | [[Category:初等幾何学]] |
| | [[Category:数学に関する記事]] | | [[Category:数学に関する記事]] |
| − | {{math-stub}}
| |