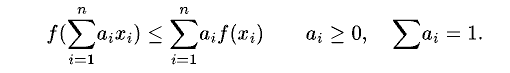|
|
| 1行目: |
1行目: |
| − | '''イェンセンの不等式'''(いぇんせんのふとうしき、{{lang-en|Jensen's inequality}})は、[[凸関数]]を使った[[不等式]]である。 | + | '''イェンセンの不等式'''(いぇんせんのふとうしき、{{lang-en|Jensen's inequality}}) |
| − | | |
| − | ''f''(''x'') を実数上の[[凸関数]]とする。
| |
| − | | |
| − | '''離散の場合''':
| |
| − | | |
| − | <math>p_1, \, p_2, \, \ldots</math> を、<math>p_1 + p_2 + \cdots = 1</math> を満たす正の実数の列とする。また、<math>x_1, \, x_2, \, \ldots</math> を、実数の列とする。そのとき、次が成り立つ。
| |
| − | | |
| − | :<math>\sum_{i=1}^{\infty} p_i f(x_i) \ge f\left( \sum_{i=1}^{\infty} p_i x_i \right)</math>
| |
| − | | |
| − | '''連続値の場合''':
| |
| − | | |
| − | <math>p(x)(>0)</math> を、<math>\int p(x) dx = 1</math> を満たす実数上の可積分関数とする。また、<math>y(x)</math> を実数上の可積分関数とする。そのとき、次が成り立つ。
| |
| − | | |
| − | :<math>\int_{-\infty}^{\infty} f(y(x))p(x) dx \ge f \left( \int_{-\infty}^{\infty} y(x)p(x) dx \right)</math>
| |
| − | | |
| − | ルベーグ積分論の観点では、 離散の場合も連続の場合も同一に見倣せる。
| |
| − | | |
| − | 証明は、''f'' の<math>\int_{-\infty}^{\infty} y(x)p(x) dx</math>における接線を ''g'' とおいて、常に ''g''(''x'') が ''f''(''x'') よりも小さいことを使えばよい。
| |
| − | | |
| − | [[統計学]]において、式の下限を評価するさいに、一定の役割を担っている。例えば、[[カルバック・ライブラー情報量|カルバックライブラーダイバージェンス]]が常に 0 より大きいことを証明するときに用いられる。''p''(''x'') が[[確率密度関数]]の場合を考えると、イェンセンの不等式は次のように書ける。
| |
| − | | |
| − | :<math>E[f(y)] \ge f(E[y])</math>
| |
| − | | |
| − | なお、イェンセンの不等式から、相加相乗平均の不等式などを導くこともできる。
| |
| − | | |
| − | ==参考文献==
| |
| − | *{{cite book|author=David Chandler|title=Introduction to Modern Statistical Mechanics|publisher=Oxford|year=1987|isbn=0-19-504277-8}}
| |
| − | * Tristan Needham (1993) "A Visual Explanation of Jensen's Inequality", American Mathematical Monthly 100(8):768–71.
| |
| − | *{{cite book|author=Walter Rudin|title=Real and Complex Analysis|publisher=McGraw-Hill|year=1987|isbn=0-07-054234-1}}
| |
| − | | |
| − | ==関連項目==
| |
| − | * [[ヨハン・イェンセン]]
| |
| | | | |
| | + | (1) 凸関数に対する不等式</p> |
| | + | <p class="meaning"> |
| | + | [[ファイル:イェンセンの不等式.gif|中央]] |
| | + | </p> |
| | + | <p class="meaning">(2) <i>a</i><sub>1</sub>, …, <i>a</i><sub><i>n</i></sub>>0 のとき, (<i>a</i><sub>1</sub><sup><i>s</i></sup>+…+<i>a</i><sub><i>ns</i></sub>)<sup>1/<i>s</i></sup> は <i>s</i> の減少関数であるという不等式.</p> |
| | {{DEFAULTSORT:いえんせんのふとうしき}} | | {{DEFAULTSORT:いえんせんのふとうしき}} |
| | | | |
イェンセンの不等式(いぇんせんのふとうしき、英語: Jensen's inequality)
(1) 凸関数に対する不等式
(2) a1, …, an>0 のとき, (a1s+…+ans)1/s は s の減少関数であるという不等式.